四种典型的递推关系

　　在所有的递推关系中，Fibonacci数列应该是最为大家所熟悉的。在最基础的程序设计语言Logo语言中，就有很多这类的题目。而在较为复杂的Basic、Pascal、C语言中，Fibonacci数列类的题目因为解法相对容易一些，逐渐退出了竞赛的舞台。可是这不等于说Fibonacci数列没有研究价值，恰恰相反，一些此类的题目还是能给我们一定的启发的。

　　Fibonacci数列的代表问题是由意大利著名数学家Fibonacci于1202年提出的“兔子繁殖问题”(又称“Fibonacci问题”)。

　　问题的提出：有雌雄一对兔子，假定过两个月便可繁殖雌雄各一的一对小兔子。问过n个月后共有多少对兔子？

　　解：设满x个月共有兔子Fx对，其中当月新生的兔子数目为Nx对。第x-1个月留下的兔子数目设为Ox对。则：

　　问题的提出：Hanoi塔由n个大小不同的圆盘和三根木柱a,b,c组成。开始时，这n个圆盘由大到小依次套在a柱上，如图1所示。

　　解：设hn为n 个盘子从a柱移到c柱所需移动的盘次。显然，当n=1时，只需把a 柱上的盘子直接移动到c柱就可以了，故h1=1。当n=2时，先将a柱上面的小盘子移动到b柱上去；然后将大盘子从a柱移到c 柱；最后，将b柱上的小盘子移到c柱上，共记3个盘次，故h2=3。以此类推，当a柱上有n(n2)个盘子时，总是先借助c柱把上面的n-1个盘子移动到b柱上，然后把a柱最下面的盘子移动到c柱上；再借助a柱把b柱上的n-1个盘子移动到c柱上；总共移动hn-1+1+hn-1个盘次。

　　问题的提出：设有n条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点，问这些封闭曲线把平面分割成的区域个数。

　　解：设an为n条封闭曲线把平面分割成的区域个数。 由图2可以看出：a2-a1=2；a3-a2=4；

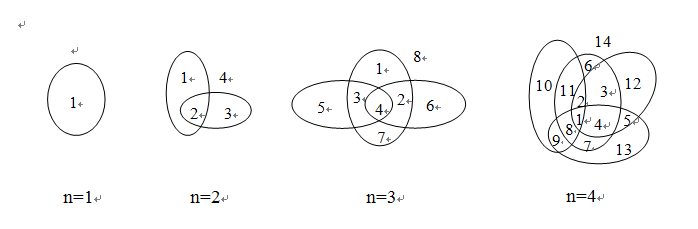
　　a4-a3=6。从这些式子中可以看出an-an-1=2(n-1)。当然，上面的式子只是我们通过观察4幅图后得出的结论，它的正确性尚不能保证。下面不妨让我们来试着证明一下。当平面上已有n-1条曲线个区域后，第n-1条曲线每与曲线相交一次，就会增加一个区域，因为平面上已有了n-1条封闭曲线，且第n条曲线与已有的每一条闭曲线恰好相交于两点，且不会与任两条曲线交于同一点，故平面上一共增加2(n-1)个区域，加上已有的an-1个区域，一共有an-1+2(n-1)个区域。所以本题的递推关系是an=an-1+2(n-1)，边界条件是a1=1。

　　n表之，hn即为Catalan数。例如五边形有如下五种拆分方案(图6-4)，故h5=5。求对于一个任意的凸n边形相应的hn。

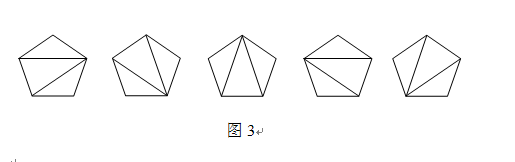
　　n表示凸n边形的拆分方案总数。由题目中的要求可知一个凸n边形的任意一条边都必然是一个三角形的一条边，边P1Pn也不例外，

　　共同构成一个三角形的三个顶点，就将n边形分成了三个不相交的部分(如图3所示)，我们分别称之为区域①、区域②、区域③，其中区域③必定是一个三角形，区域①是一个凸k边形，区域②是一个凸n-k+1边形，区域①的拆分方案总数是C

　　小结：通过上面对四种典型的递推关系建立过程的探讨，可知对待递推类的题目，要具体情况具体分析，通过找到某状态与其前面状态的联系，建立相应的递推关系。

　　例1、在一个正六边形的六个区域中的每一个区域染上红、黄、蓝、紫四种颜色之一，要求相邻的两个区域染色不相同，则有多少种不同的染色方法？